
Ulugbek S. Kamilov
Research Scientist
Computational Sensing
Mitsubishi Electric Research Laboratories (MERL)
201 Broadway, 8th Floor
Cambridge, MA 02139, USA

Computational Sensing
Mitsubishi Electric Research Laboratories (MERL)
201 Broadway, 8th Floor
Cambridge, MA 02139, USA
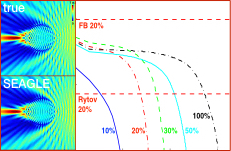
Linear scattering models assume weakly scattering objects, making corresponding imaging methods inherently inaccurate for many applications. This places fundamental limits—in terms of resolution, penetration, and quality—on the imaging systems relying on such models. We developed a new computational imaging method called SEAGLE that combines a nonlinear scattering model and a total variation (TV) regularized inversion algorithm. The key benefit of SEAGLE is its efficiency and stability, even for objects with large permittivity contrasts. This makes SEAGLE suitable for robust imaging under multiple scattering.

Multimodal imaging is becoming increasingly important in a number of applications, providing new capabilities and new processing challenges. My team is investigating the benefit of combining multiple sensors for obtaining a high-quality multimodal view of an object. Our latest formulation incorporates temporal information and exploits the motion of objects in video sequences to significantly improve the quality of captured multimodal images.
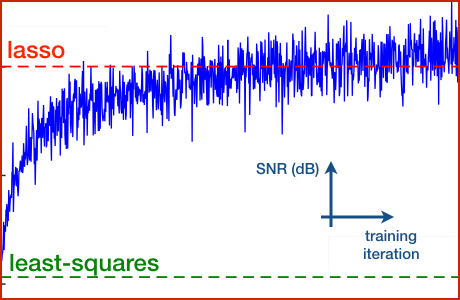
Proximal-gradient methods are extremely popular due to their ability to seamlessly combine the knowledge of data formation with the prior information on the signal. A key feature of such approaches is that both data-fidelity term and the regularizer are manually designed in an attempt to capture the statistical distribution of natural signals. One of our recent research areas is to study how some core ideas from Deep Learning can be used for designing optimal imaging methods directly from data.
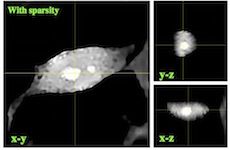
Optical Diffraction Tomography (ODT) is the one of the most popular technique for 3D imaging of biological samples. Learning Tomography (LT) is our novel extension of ODT that can numerically form images of 3D bilogical samples in the presence of multiple scattering. Our techique formulates the measurement model as an artificial multilayer neural network and relies on total variation (TV) regularization for forming high-quality images under few noisy measurements. We demonstrated the methods experimentally by imaging HeLa and hTERT-RPE1 cells.
Our work is motivated by the recent trend whereby classical linear methods are being replaced by nonlinear alternatives that rely on the sparsity of naturally occurring signals. We adopt a statistical perspective and model the signal as a realization of a stochastic process that exhibits sparsity as its central property. Our general strategy for solving inverse problems then lies in the development of novel iterative solutions for performing the statistical estimation. Specifically, we explore methods based on belief propagation method and its approximation in the form of approximate message passing.

Estimation of a vector from quantized linear measurements is a common problem for which simple linear techniques are suboptimal—sometimes greatly so. We have developed message-passing de-quantization (MPDQ) algorithms for minimum mean-squared error estimation of a random vector from quantized linear measurements, notably allowing the linear expansion to be overcomplete or undercomplete and the scalar quantization to be regular or non-regular. The algorithm is based on generalized approximate message passing (GAMP), a Gaussian approximation of loopy belief propagation for estimation with linear transforms and nonlinear componentwise-separable output channels. For MPDQ, scalar quantization of measurements is incorporated into the output channel formalism, leading to the first tractable and effective method for high-dimensional estimation problems involving non-regular scalar quantization. The algorithm is computationally simple and can incorporate arbitrary separable priors on the input vector including sparsity-inducing priors that arise in the context of compressed sensing.

We provide a theoretical justification for the popular wavelet-domain estimation technique called cycle spinning in the context of general linear inverse problems. Cycle spinning has been extensively used for improving the visual quality of images reconstructed with wavelet-domain methods. We also refine traditional cycle spinning by introducing the concept of consistent cycle spinning that can be used to perform wavelet-domain statistical estimation. In particular, we empirically show that consistent cycle spinning achieves the minimum mean-squared error (MMSE) solution for denoising stochastic signals with sparse derivatives.